生成モデル $G$ によって生成されるサンプルを訓練データのサンプルであると, 識別モデル $D$ が誤認するように学習を進めていく GAN. 貨幣の偽造者 (counterfeiter) と警察 (police) などのアナロジーから, 発想自体は直感的で理解しやすい.

価値関数 $V(G,D)$ の導入

$G$ と $D$ による価値関数 $V(G,D)$ のミニマックスゲームが GAN である.

— 記法 —

• データ変数 $\mathbf{x}$: 真の分布 $p_{\mathrm{data}}(\mathbf{x})$ によりサンプルされる.
• ノイズ変数 $\mathbf{z}$: 事前分布 $p_{\mathbf{z}}(\mathbf{z})$ によりサンプルされる.
• 生成モデル $G$: パラメータ $\theta_g$ の多層パーセプトロン (MLP) によって表現された, 微分可能な生成関数 $G(\mathbf{z};\theta_g): \mathbf{z}↦\mathbf{x}$ により, 生成分布 $p_g(\mathbf{x})$ を出力する.
• 識別モデル $D$: パラメータ $\theta_d$ の MLP によって表現された, 定値な識別関数 $D(\mathbf{x};\theta_d): \mathbf{x}↦[0,1]∈\mathbb{R}$ により, $\mathbf{x}$ が訓練データから来ている確率を出力する.

— ミニマックスゲームの定式化 —

下図がこのミニマックスゲームによる訓練の概要だが, 以下これを理論的に保証する.

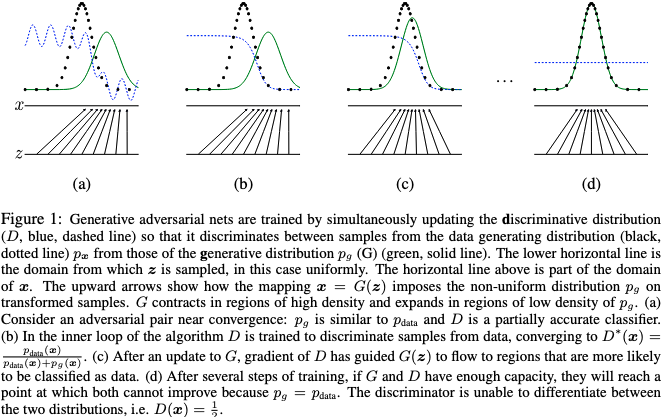
ミニマックスゲームの大域解とアルゴリズムの収束性

ミニマックスゲームによる訓練アルゴリズムが大域的な一意最適解に収束することを示す.

GAN のミニバッチ SGD 訓練アルゴリズム

命題 2 によって収束性が保証される GAN の最終的な訓練アルゴリズム. 実際は $G$ を MLP とすると $V(G,D)$ は非凸になるので以下の議論は成り立たないが, それでも実用上うまくいくことが実験結果を見ればわかる. しかし, 非凸性に起因するモード崩壊やミニマックスゲームの定式化に起因する訓練初期の勾配消失などが, GAN による学習の不安定性を招くこともまた事実である.

大域的一意最適解 $-\log 4$ の存在

定理 1 によりこれを示す (補題 1 は勝手に加えた) .

命題 1. $G$ を固定したとき, $D$ の最適解は次の表式で与えられる.

証明. 与えられた任意の $G$ に対し, $D$ の最適化は次の価値関数の最大化をもってして行われる.

一般に, $∀(a,b)∈\mathbb{R}^2\setminus\{0,0\},$ 関数 $y→a\log(y)+b\log(1-y)$ は $\frac{a}{a+b}$ において最大値をとる ($\log$ の定義域より当然 $y∈[0,1]$). この場合, $\mathrm{Supp}(p_{\mathrm{data}})∪\mathrm{Supp}(p_g)$ の外ではサンプルが現れず $V$ に寄与しないことから, $D$ の定義域をそれらの台の上に限定してよい, $\mathrm{i.e.}$, $(p_{\mathrm{data}},p_g)∈\mathbb{R}^2\setminus\{0,0\}$. よって示された. $\square$

補題 1. 価値関数を $p_g$ の関数として捉え, $V(G,D)≔U(p_g,D)$ とおけば, $V(G,D_G^*)=\mathop{\sup}\limits_{D}U(p_g,D)$ であり, $U(p_g,D)$ は $p_g$ に関して凸.

証明. 価値関数の場合, 最大値が存在すればそれは上限と一致するので, $V(G,D_G^*)=\mathop{\sup}\limits_{D}U(p_g,D)$. また,

だから, $U(p_g,D)$ は第 2 項 においてのみ $p_g$ 依存性を持つ. その依存性は,

と $p_g$ に関して線形である. 一方, 第 1 項は $p_g$ 依存性から見れば定数であるから, $U(p_g,D)$ は $p_g$ についての Affine 関数である. Affine 関数は凸関数, かつ凹関数であるので, これにより補題が示された. $\square$

定理 1. $V(G,D_G^*)$ が大域的最小値を取るのは $p_g=p_{\mathrm{data}}$ のとき, またそのときに限る. そしてその値は $-\log 4$ である.

証明. 命題 1 により $V(G,D_G^*)$ は次のように変形される.

ここで, $D_{JS}\left(p_{\mathrm{data}}(\mathbf{x})||p_g(\mathbf{x})\right)≥0$ であり, $0$ となるのは $p_g=p_{\mathrm{data}}$ のとき, またそのときに限る. したがって $V(G,D_G^*)≥-\log 4$ であり, 最小値 $-\log 4$ をとるのは $p_g=p_{\mathrm{data}}$ のとき, またそのときに限ることが示された. またここにおいて, 補題 1 より $V(G,D_G^*)$ の最適化はいわゆる凸最適化の問題であることが示されたため, 最適化されたときにとる最小値は必ず大域解となる. 以上により示された. $\square$

アルゴリズム 1 の収束性

命題 2. 次の 3 つの仮定の下で, アルゴリズム 1 により $p_g$ は $p_{\mathrm{data}}$ に収束する.

1. $G$ と $D$ が十分な容量を持つ.
2. アルゴリズム 1 の各ステップで, 与えられた $G$ に対し, $D$ はその最適解に到達することが可能.
3. それを受けて, $p_g$ は $\mathop{\sup}\limits_{D}U(p_g,D)$ を最適化するように更新される.

証明. 一般に, 凸関数 $f$ の上限の劣微分は, 最大値をとる点においてその関数の微分を含む, $\mathrm{i.e.}$, $∂f_{\beta}(x)∈∂_{\mathrm{sub}}\mathop{\sup}\limits_{\alpha∈\mathcal{A}}f_{\alpha}(x)\space\space\mathrm{if}\space\space\beta=\arg\mathop{\sup}\limits_{\alpha∈\mathcal{A}}f_{\alpha}(x)$. したがって $U(p_g,D)$ は $p_g$ に関して凸 (補題 1) であるから, 次が成り立つ.

つまり左辺による最適化は右辺による最適化によっても達成される. ゆえに仮定 1-3 のもと, アルゴリズム 1 により $p_g$ は $p_{\mathrm{data}}$ へと収束する (定理 1). $\square$